干货：不同类型的手游出海如何打造数据模型精准预测 LTV？(内附Excel模型)

作者：Chek游戏出海总舵主

来源：Chek游戏出海总舵主（ID：masterchek）

舵主我向来办事靠谱，已经把教材都整理好了，这一期就会手把手教大家打造数据模型，对 LTV 进行精准预测，更会把当中用到的 excel 数据表和数据模型免费送给大家，倾囊相授、绝不藏私。

 *在微信公号“白鲸出海”后台回复“LTV”即可获得 excel 数据表和数据模型。

今天的课程干货满满，事不宜迟，我们赶紧开始吧！

不同的游戏，LTV 的时长和观察单位都有所不同，我们根据游戏的轻重度进行了简单分类，方便大家参考。

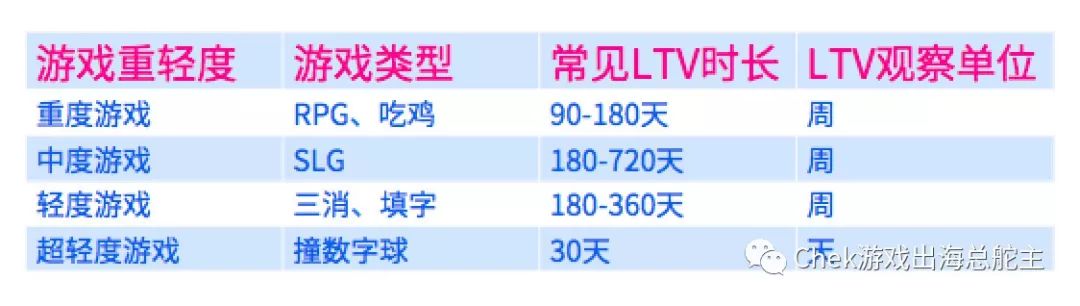
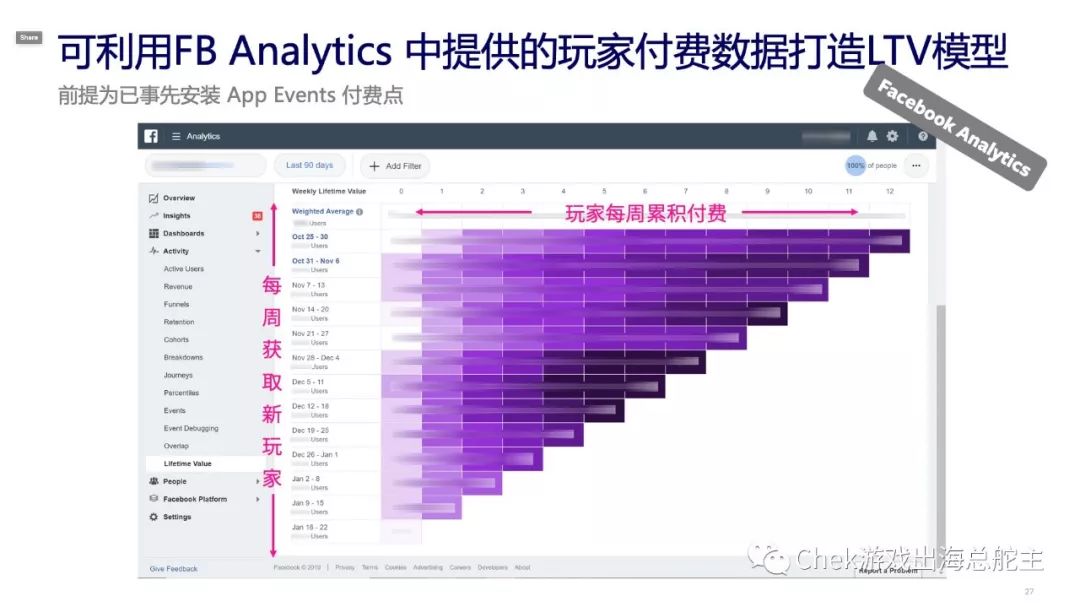
无论是哪一类游戏，我们都必须先获得一定的 LTV 数据作为基础，才能对后续的 LTV 进行预测。大家可以通过第三方后台或自己的 BI 后台获得 LTV 数据。如果没有这些后台也不要紧，只要您接入了 Facebook 的 SDK 数据(即安装了应用事件付费点)，在正确回传相应的事件及价值的情况下，便能够在 Facebook Analytics 的后台通过 lifetime value 统计功能，了解每一周新获取的玩家数量及累积的付费情况，最长可以查看过去 90 天的数据。

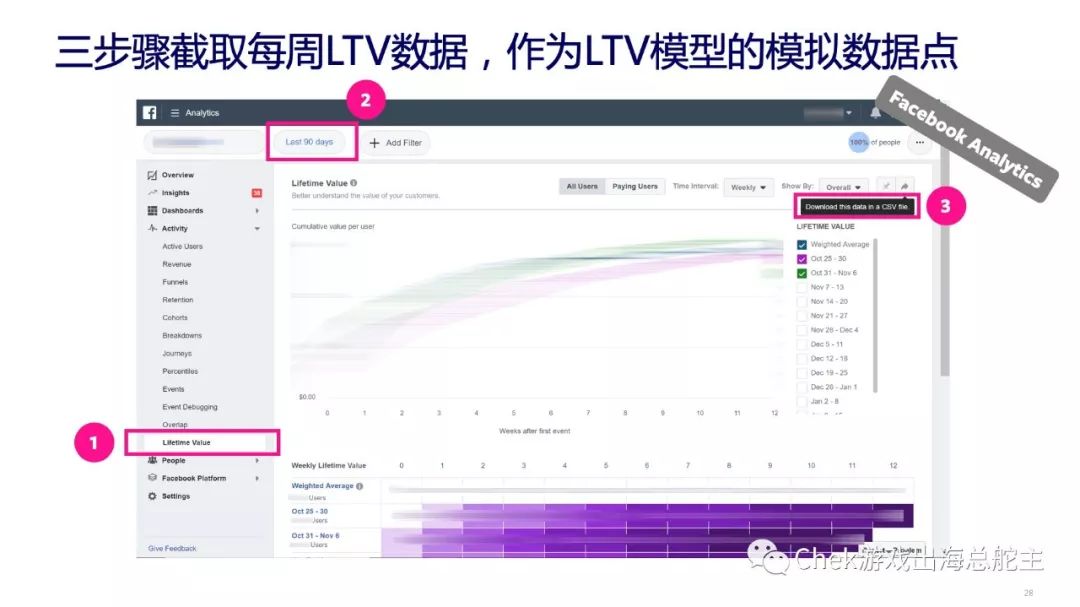
统计好相应的 LTV 数据后，可以设置较为合适的时间窗，跟着下图所示的三个步骤，把数据导出来。

接下来，就要利用导出的这些数据来预测 LTV。预测 LTV 的方法有很多，今天我们要给大家介绍的，是某手游海外推广客户在实践中亲证有效的方法。为方便大家理解，我们会使用一个模拟案例来进行说明。

首先，要对导出的数据进行筛选，要确保获得足够的数据；其次，要确保数据在变化时的稳定性。

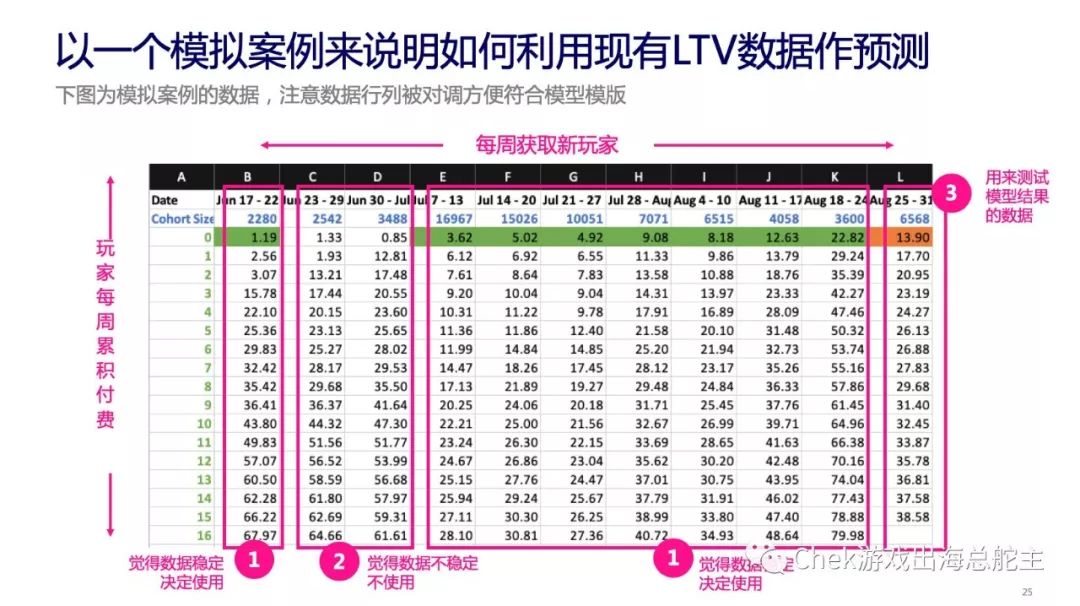
以上图为例，最上面那一行的日期是以周为单位，第二行蓝色的 cohort size 则是指这周获取的新玩家数量；最左边 0 到 16 那列绿色数字指的是，新玩家进行游戏的周数，旁边第二列的黑色数字则指上面日期内获取的新玩家在开始游戏后相应周数的 LTV。比如 6 月 17 日到 22 日有 2280 名新玩家，他们刚开始游戏的付费值为 1.19 元/美元，到了第 1 周付费值则累积至 2.56 元/美元。

如图所示，由于 6 月 23 日至 29 日以及 6 月 30 日至 7 月 6 日这两周数据前面的跳跃幅度较大，累积增长情况不够稳定，为免影响预测结果的精确度，我们决定不使用这两周的数据。

选取好数据之后，如何把数据输入到模版上去呢？

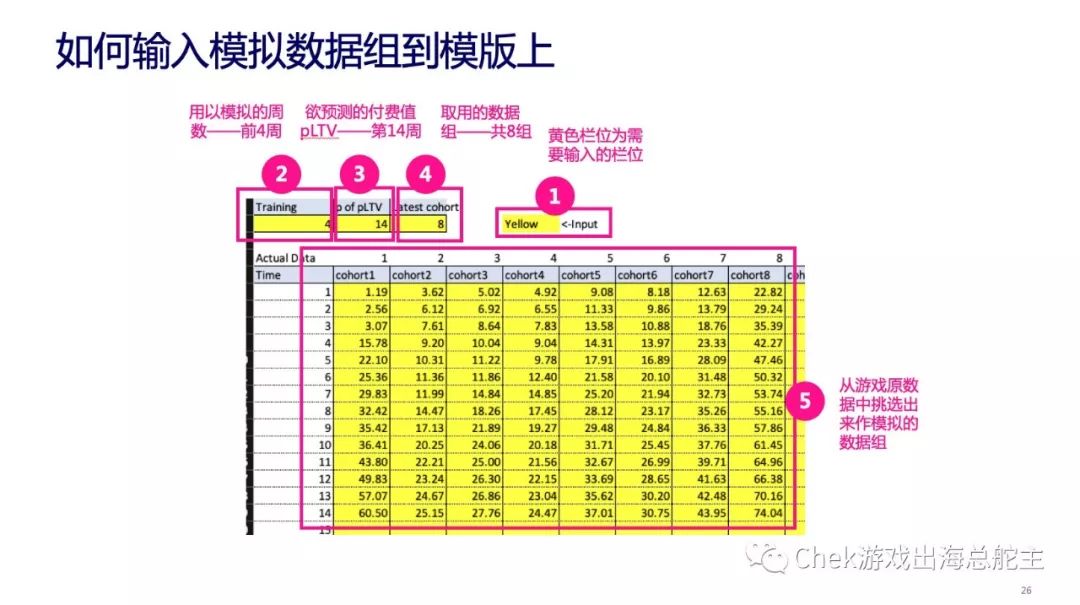
以上图为例，在去掉不稳定数据后，我们一共获得 8 组玩家的数据样本，输入到图中标黄的位置。然后分别选取每组玩家前四周的付费数据（即在 excel 表格的 Training 中输入 4），用于预测第 14 周的 pLTV（预测玩家终身价值）（即在 excel 的 p of pLTV 中输入 14）。 

由于我们提供的数据里已经包括了第 14 周的真实 LTV，可供参照，所以这个模型还可以计算预测结果和实际数据之间的误差，并进行误差修正，让这个模型更为精确、智能。

由于第 1 到第 8 组是根据每周时间的推移不断递增的，在这个表格里，第 8 组（cohort 8）的玩家是最新获取的，因此我们需要把 Latest Cohort 设置为 8，让模型知道这组数据是最新的。为什么要这么做，我们下面就会讲解到。

我们可以使用三种不同的函数曲线（包括幂函数、对数函数和线性函数）来预测 LTV，找到最搭配的函数建立 LTV 模型。这三种函数也包含在了我们提供的 excel 当中，方便大家使用。

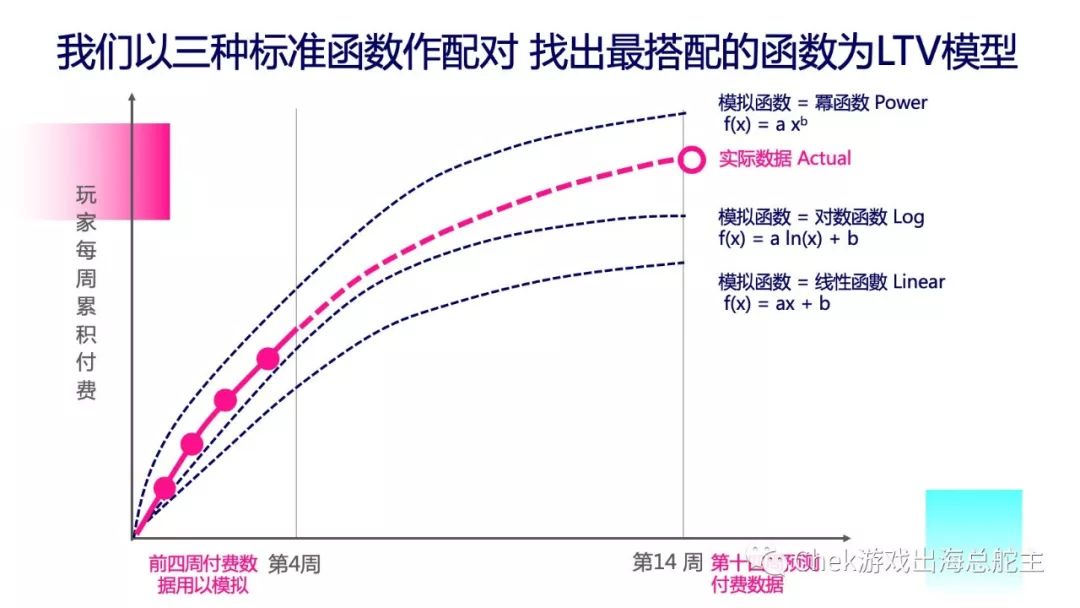
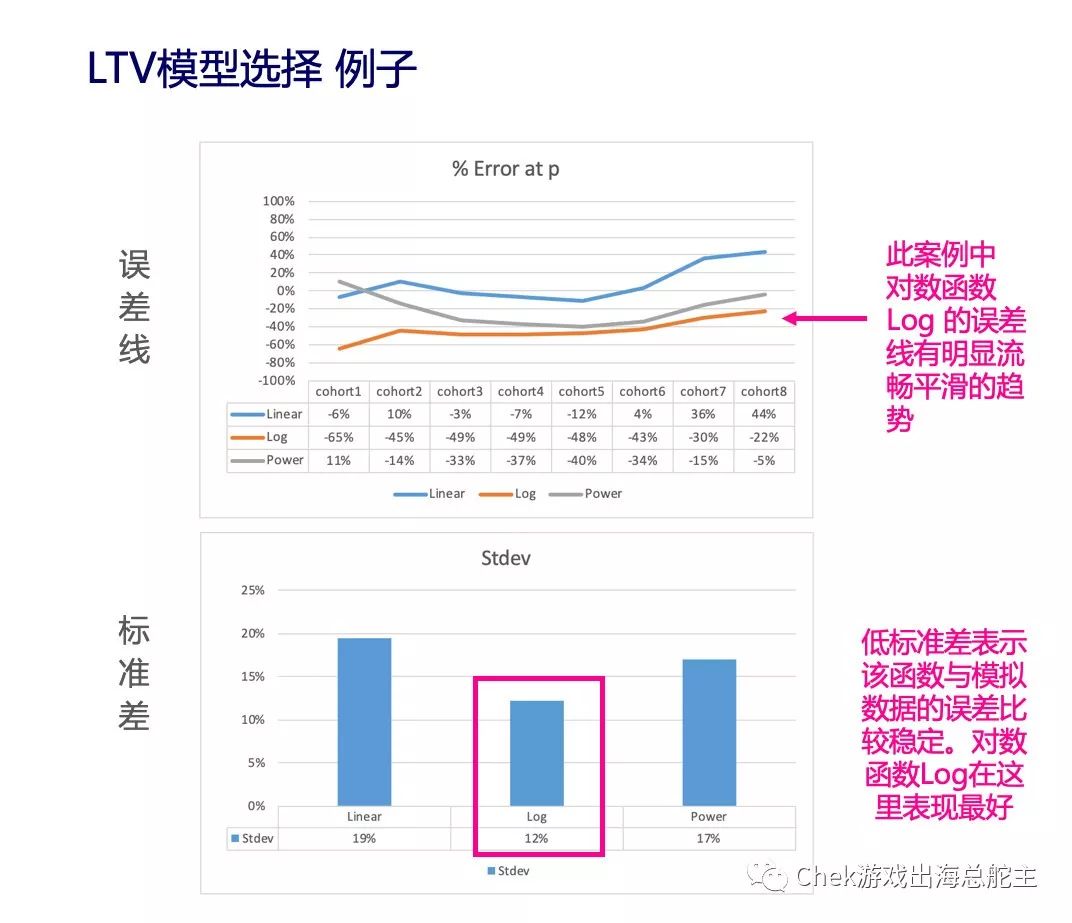
上图则是使用这三种模拟函数预测的 LTV 变化曲线和实际数据曲线的对比一览图 (此数据纯属虚构，旨在提供一个概念)。

为了对比三种模拟函数孰优孰劣，我们需要介绍两个概念——误差线和标准差。

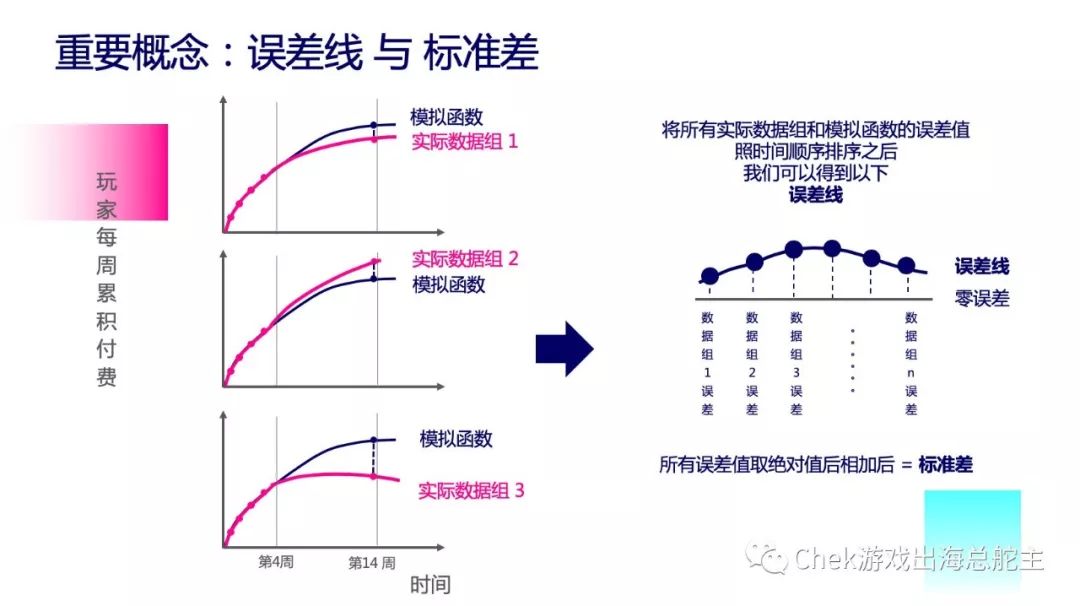
误差线：

由于我们是以 8 组玩家在前 4 周的数据为基础，对 LTV 进行预测，在这 8 组数据当中，每一种模拟函数预测的 LTV 和实际数据都存在误差，将 8 组实际数据组和模拟函数的误差值照时间顺序排序之后，就可以连成一条线（如上图右边所示），这条线就是误差线。

标准线：

把所有误差值取绝对值后相加，就能够得到标准差。标准差越小，说明这个模型越趋近于零误差，能够预测出来的 LTV 也就更加精确。

误差线和标准差这两个指标，有助于我们选取一个相对更为精准的 LTV 预测模型。

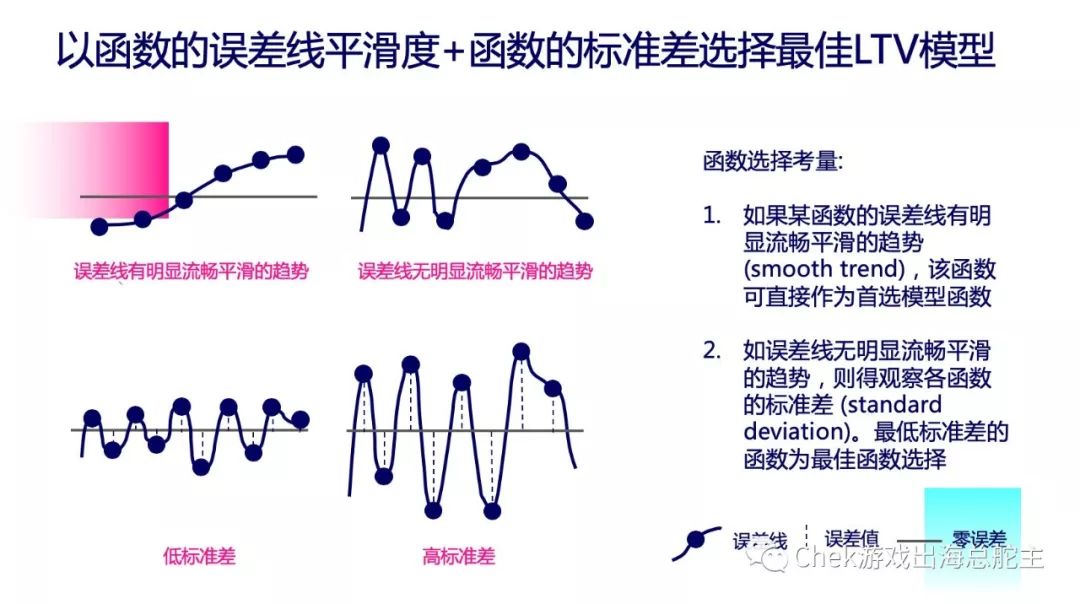
. 首先看误差线的平滑度：如果某函数的误差线有明显流畅平滑的趋势，则表明这个函数模型和实际数据之间的误差保持在一定可控的范围内，该函数可直接作为首选模型函数。

. 其次再看标准差：如果误差线没有明显流畅平滑的趋势，再来观察各函数的标准差，最低标准差的函数为最佳选择。

以刚刚的三组函数模型为例，观察下图可发现，对比线性函数（Linear）、对数函数（Log）和幂函数（Power）三条函数曲线，对数函数的误差线更为流畅平滑，加上对数函数的标准差也是最低的，说明对数函数模型是最佳选择。当然在其他案例中，平滑的误差线不一定同时完美具备最低的标准差，这时还是得参考以上的考量顺序。

模型和实际数据之间难免会存在误差，所以必须要对预测的数据进行修正。接下来，我们就要讲解如何为 LTV 模型选择最佳修正值。

. 当函数因误差线流畅平滑获选时：由于最新获得那组数据（即cohort 8）最能反映之后的趋势和走向，表现出来的误差也会最小，所以要使用最新误差（Latest Error）来修正模型。

. 当函数因标准差较小获选时：需要使用平均误差（Average Error）作为修正值。

在这个例子当中，由于对数函数主要是因为曲线明显流畅平滑而获选，所以我们使用了最新误差(Latest Error) 来进行修正。

最后我们再总结一下，如何在实践中使用今天分享的 LTV 模型，主要包括如下图所示的四个方面。

1、选择用于模拟的周数（在我们的例子当中即前 4 周），以及希望预测 LTV 的周数（即第 14 周）

2、输入希望预测 LTV 的前几周数据（即前 4 周的数据），然后套用三种函数模型对之后的 LTV 进行预测，便会得到图中间下方 pLTV 那组数据，而图中间上方则是三个函数的误差表现，在我们的案例当中，选择的是曲线最为流畅平滑的对数函数（Log）。

3、选择较为理想的修正值，在例子中使用的是最新误差（Latest Error）。

4、最后便能得到修正后的预测付费值 pLTV：以对数函数这组数据为例，第 14 周的 pLTV 在修正后，从原先的 31.3 变成了 40.3，而下面的 Optimistic 和 Pessimistic 这两行则分别代表了预测付费值 pLTV 的大致波动范围，即最高可能会升到 47.8， 最低则可能跌至 34.9。

通过科学模型精准预测 LTV，我们便能对玩家终身价值的变化趋势有更为深刻的了解，从而更好地指导及调整营销策略。

如果预测付费值 pLTV 强劲：表示用于获取玩家的成本极可能会给您带来更高的收益，因此可以拿出更多预算进行营销，抢占市场，包括：

. 加大投放力度

. 提高出价

如果预测付费值 pLTV 较弱：证明营销策略可能存在一定问题，要适当调整，包括：

. 制作广告吸引老玩家回流

. 提高游戏内购水平

. 改变定位与素材方向

. 使用价值导向产品获取更多付费玩家，提高广告花费回报：如 AEO、VO、VBLAL 等定位或优化方式

文中案例所使用的数学模型的 excel 文件，供您参考，建立起最适合自己的 LTV 预测模型。